Simulations with UK Biobank genotypes, missing phenotypic values, and different effect structure across traits
Fabio Morgante & Deborah Kunkel
August 20, 2024
Last updated: 2024-08-20
Checks: 7 0
Knit directory: mr_mash_rss/
This reproducible R Markdown analysis was created with workflowr (version 1.7.0). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.
Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
The command set.seed(20230612) was run prior to running
the code in the R Markdown file. Setting a seed ensures that any results
that rely on randomness, e.g. subsampling or permutations, are
reproducible.
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.
Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.
The results in this page were generated with repository version a622531. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.
Note that you need to be careful to ensure that all relevant files for
the analysis have been committed to Git prior to generating the results
(you can use wflow_publish or
wflow_git_commit). workflowr only checks the R Markdown
file, but you know if there are other scripts or data files that it
depends on. Below is the status of the Git repository when the results
were generated:
Ignored files:
Ignored: .snakemake/
Ignored: data/
Ignored: output/GWAS_for_regions/
Ignored: output/bayesC_fit/
Ignored: output/bayesR_fit/
Ignored: output/estimated_effects/
Ignored: output/kriging_rss_fit/
Ignored: output/ldpred2_auto_fit/
Ignored: output/ldpred2_auto_gwide_fit/
Ignored: output/ldsc_fit/
Ignored: output/misc/
Ignored: output/mr_mash_rss_fit/
Ignored: output/mtag_ldpred2_auto_fit/
Ignored: output/mtag_summary_statistics/
Ignored: output/mvbayesC_fit/
Ignored: output/prediction_accuracy/
Ignored: output/sblup_fit/
Ignored: output/summary_statistics/
Ignored: output/wmt_sblup_fit/
Ignored: run/
Ignored: tmp/
Untracked files:
Untracked: code/adjust_LD_test.R
Untracked: code/compute_sumstats_test_bc_ukb.R
Untracked: code/compute_sumstats_ukb_2.R
Untracked: code/fit_kriging_rss_ukb.R
Untracked: code/fit_mrmashrss_test_ukb.R
Untracked: code/match_sumstats_with_LD_ukb.R
Untracked: code/merge_sumstats_all_chr_ukb.R
Untracked: code/split_effects_by_chr_imp_ukb.R
Untracked: scripts/11_run_fit_mrmashrss_by_chr_V_all_chr_bc_ukb.sbatch
Untracked: scripts/11_run_fit_mrmashrss_sparse_LD_mvsusie_paper_prior_by_chr_bc_ukb.sbatch
Untracked: scripts/12_run_compute_pred_accuracy_mrmashrss_sparse_LD_mvsusie_paper_prior_bc_ukb.sbatch
Untracked: scripts/12_run_fit_mrmashrss_sparse_LD_Vcor_all_chr_init_by_chr_bc_ukb.sbatch
Untracked: scripts/13_run_compute_pred_accuracy_mrmashrss_sparse_LD_Vcor_all_chr_init_bc_ukb.sbatch
Untracked: scripts/3_run_compute_sumstats_by_chr_and_fold_test_bc_ukb.sbatch
Untracked: scripts/7_run_compute_residual_cor_all_chr_bc_ukb.sbatch
Untracked: scripts/run_adjust_LD_test.sbatch
Untracked: scripts/run_fit_kriging_rss_by_chr_and_trait_bc_ukb.sbatch
Untracked: vs_sm_convert/
Untracked: vs_sm_test/
Unstaged changes:
Modified: analysis/index.Rmd
Modified: ukb_real_data_ot.yaml
Modified: ukb_real_data_ot_initiator.sh
Modified: ukb_real_data_ot_snakefile
Modified: ukb_sim_missing_pheno_equal_effects_indep_resid.yaml
Modified: ukb_sim_missing_pheno_snakemake_submitter.sh
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
These are the previous versions of the repository in which changes were
made to the R Markdown
(analysis/ukb_sim_missing_pheno_results.Rmd) and HTML
(docs/ukb_sim_missing_pheno_results.html) files. If you’ve
configured a remote Git repository (see ?wflow_git_remote),
click on the hyperlinks in the table below to view the files as they
were in that past version.
| File | Version | Author | Date | Message |
|---|---|---|---|---|
| Rmd | a622531 | fmorgante | 2024-08-20 | Update results |
| html | 597bd1f | fmorgante | 2024-08-19 | Build site. |
| Rmd | 6131dbc | fmorgante | 2024-08-19 | Fix typo |
| html | c8b1982 | fmorgante | 2024-08-19 | Build site. |
| Rmd | 43a7cb4 | fmorgante | 2024-08-19 | Update results with missing values |
| html | bb30b9e | fmorgante | 2024-08-16 | Build site. |
| Rmd | 82c2d69 | fmorgante | 2024-08-16 | Add results with missing values |
###Load libraries
library(ggplot2)
library(cowplot)
metric <- "r2"
traitz <- 1:5Introduction
The goal of this analysis is to benchmark the newly developed mr.mash.rss (aka mr.mash with summary data) against already existing methods in the task of predicting phenotypes from genotypes using only summary data. To do so, we used real genotypes from the array data of the UK Biobank. We randomly sampled 105,000 nominally unrelated (\(r_A\) < 0.025 between any pair) individuals of European ancestry (i.e., Caucasian and white British fields). After retaining variants with minor allele frequency (MAF) > 0.01, minor allele count (MAC) > 5, genotype missing rate < 0.1 and Hardy-Weinberg Equilibrium (HWE) test p-value > \(1 *10^{-10}\), our data consisted of 595,071 genetic variants (i.e., our predictors). Missing genotypes were imputed with the mean genotype for the respective genetic variant.
The linkage disequilibrium (LD) matrices (i.e., the correlation matrices) were computed using 146,288 nominally unrelated (\(r_A\) < 0.025 between any pair) individuals of European ancestry (i.e., Caucasian and white British fields), that did not overlap with the 105,000 individuals used for the rest of the analyses.
For each replicate, we simulated 5 traits (i.e., our responses) by randomly sampling 5,000 variants (out of the total of 595,071) to be causal, with different effect sharing structures across traits (see below). The genetic effects explain 50% of the total per-trait variance (except for two scenario as explained below) – in genetics terminology this is called genomic heritability (\(h_g^2\)). The residuals are uncorrelated across traits. Each trait was quantile normalized before all the analyses were performed.
We randomly sampled 5,000 (out of the 105,000) individuals to be the test set. The test set was only used to evaluate prediction accuracy. All the other steps were carried out on the training set of 100,000 individuals.
We assigned missing values completely at random (MCAR) to the phenotype matrix for the training individuals.
Summary statistics (i.e., effect size and its standard error) were obtained by univariate simple linear regression of each trait on each variant, one at a time. Variants were not standardized.
A few different methods were fitted:
- LDpred2 per-chromosome with the auto option, 1000 iterations (after 500 burn-in iterations), \(h^2\) initialized using an estimate from LD Score regression (LDSC) and \(p\) initialized using the same grid as in the original paper. NB this is a univariate method.
- mr.mash.rss per-chromosome, with both canonical and data-driven covariance matrices computed as described in the mvSuSiE paper, updating the (full rank) residual covariance and the mixture weights, without standardizing the variables. The residual covariance was initialized as in the mvSuSiE paper and the mixture weights were initialized as 90% of the weight on the null component and 10% of the weight split equally across the remaining components. The phenotypic covariance was computed as the sample covariance using the individual-level data. NB this is a multivariate method.
- BayesR per-chromosome, with 5000 iterations, 1000 burn-in iterations, thinning factor of 5, \(\pi\) (i.e., the proportion of causal variants) initialized as 0.0001, \(h^2\) initialized as 0.1, and other default parameters. NB this is a univariate method. We used the implementation in the qgg R package.
- mvBayesC per-chromosome, with 5000 iterations, 1000 burn-in iterations, thinning factor of 5, \(\pi\) (i.e., the proportion of causal variants) initialized as 0.0001, \(h^2\) initialized as 0.1, and other default parameters. NB this is a multivariate method. We used the implementation in the qgg R package.
- mvBayesCrest – a version of mvBayesC that only allows a variant to affect all or none of the traits – per-chromosome, with 5000 iterations, 1000 burn-in iterations, thinning factor of 5, \(\pi\) (i.e., the proportion of causal variants) initialized as 0.0001, \(h^2\) initialized as 0.1, and other default parameters. NB this is a multivariate method. We used the implementation in the qgg R package.
- wMT-SBLUP per-chromosome, with \(M_{eff}=60000\) and SBLUP estimate obtained with a window size of 2 Mb (using the SumTool R package implementation). NB this is a multivariate method. We used the implementation in the qgg R package.
- MTAG+LDpred2 with all variants. Because MTAG does not allow analyzing small indels and our data has a small numaber of those, we kept assigned the OLS estimates to those variants (instead of dropping them) before running LDpred2. LDpred2 was run with the same parameter as above, but with “shrink_corr=0.95” and “allow_jump_sign=FALSE” to avoid convergence issues. The effective sample size was estimated from the median \(\chi^2\) statistics of the OLS estimates and the MTAG estimates as done here.
Prediction accuracy was evaluated as the \(R^2\) of the regression of true phenotypes on the predicted phenotypes. This metric as the attractive property that its upper bound is \(h_g^2\).
20 replicates for each simulation scenario were run.
Equal effects scenario, small proportion of missing values
In this scenario, the effects were drawn from a Multivariate Normal distribution with mean vector 0 and covariance matrix that achieves a per-trait variance of 1 and a correlation across traits of 1. This implies that the effects of the causal variants are equal across responses. Missing values were assigned to 20% of the individuals such that all missing value configurations across traits are equally likely for each individual. This resulted in the following proportion of missing cells in the phenotype matrix:
repz <- c(1:17, 19:21)
scenarioz <- "02_full_equal_effects_indep_resid"
prefix <- "data/phenotypes/simulated/ukb_caucasian_white_british_unrel_100000_missing_pheno"
missingness <- vector("numeric", length(repz))
i <- 0
for(repp in repz){
i <- i+1
dat <- readRDS(paste0(prefix, "_", scenarioz, "_pheno_missing_", repp, ".rds"))
missingness[i] <- dat$prop_missing_cells
}
summary(missingness) Min. 1st Qu. Median Mean 3rd Qu. Max.
0.09892 0.09932 0.09968 0.09984 0.10044 0.10104 Here’s the methods comparison.
repz <- c(1:17, 19:21)
prefix <- "output/prediction_accuracy/ukb_caucasian_white_british_unrel_100000_missing_pheno"
scenarioz <- "02_full_equal_effects_indep_resid"
methodz <- c("mr_mash_rss", "mvbayesC", "mvbayesC_rest", "wmt_sblup", "mtag_ldpred2_auto", "ldpred2_auto", "bayesR")
i <- 0
n_col <- 6
n_row <- length(repz) * length(scenarioz) * length(methodz) * length(traitz)
res <- as.data.frame(matrix(NA, ncol=n_col, nrow=n_row))
colnames(res) <- c("rep", "scenario", "method", "trait", "metric", "score")
for(sce in scenarioz){
for(met in methodz){
for(repp in repz){
dat <- readRDS(paste0(prefix, "_", sce, "_", met, "_pred_acc_", repp, ".rds"))
for(trait in traitz){
i <- i + 1
res[i, 1] <- repp
res[i, 2] <- sce
res[i, 3] <- met
res[i, 4] <- trait
res[i, 5] <- metric
res[i, 6] <- dat$r2[trait]
}
}
}
}
res <- transform(res, scenario=as.factor(scenario),
method=as.factor(method),
trait=as.factor(trait))
p_methods_shared <- ggplot(res, aes(x = trait, y = score, fill = method)) +
geom_boxplot(color = "black", outlier.size = 1, width = 0.85) +
stat_summary(fun=mean, geom="point", shape=23,
position = position_dodge2(width = 0.87,
preserve = "single")) +
ylim(0, 0.51) +
scale_fill_manual(values = c("pink", "red", "yellow", "orange", "green", "blue", "lightblue")) +
labs(x = "Trait", y = expression(italic(R)^2), fill="Method", title="") +
geom_hline(yintercept=0.5, linetype="dotted", linewidth=1, color = "black") +
theme_cowplot(font_size = 18)
print(p_methods_shared)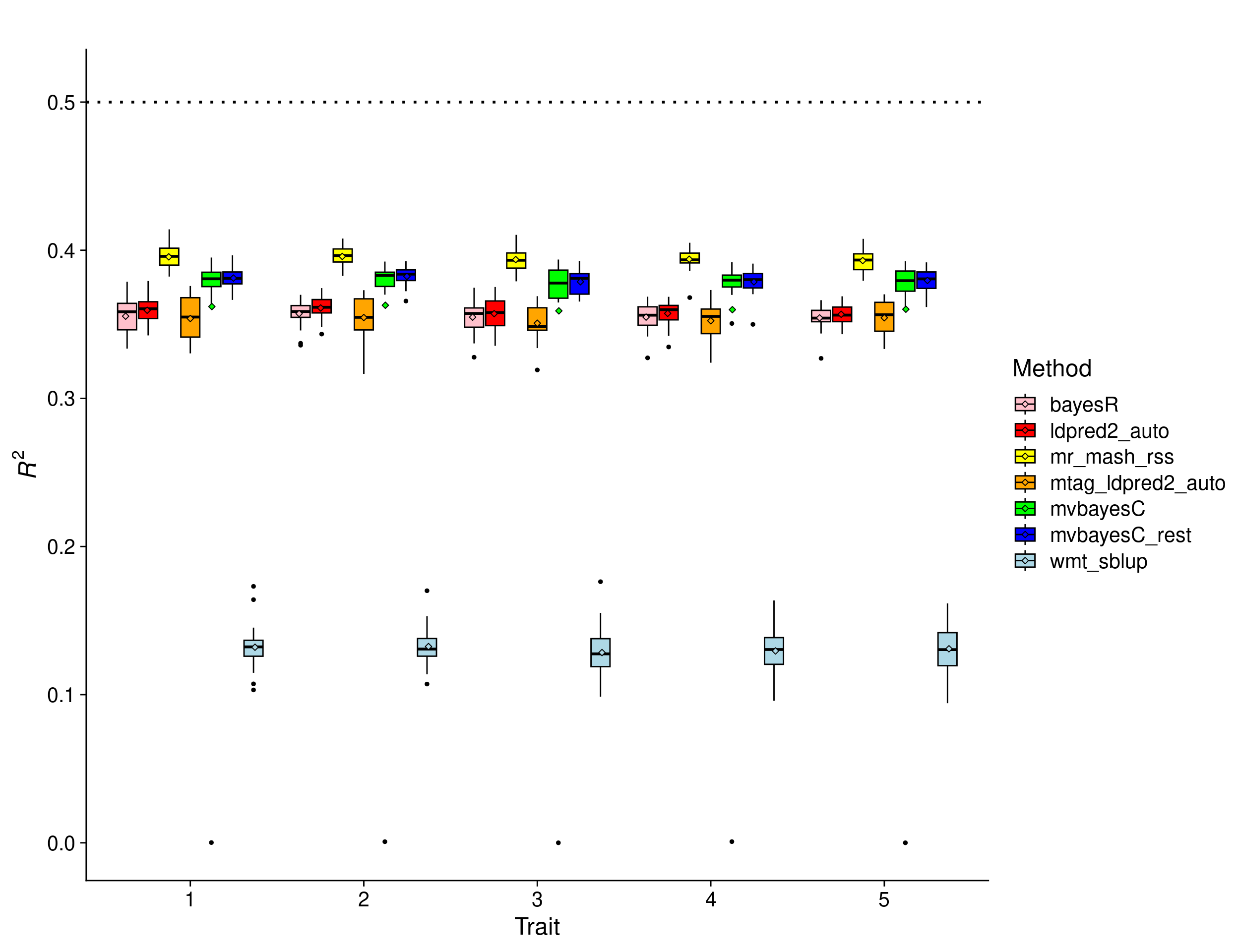
| Version | Author | Date |
|---|---|---|
| c8b1982 | fmorgante | 2024-08-19 |
The results are very similar to the equivalent scenario without missing values. This highlights that mr.mash-rss is robust to a small proportion of missing values.
Equal effects scenario, medium proportion of missing values
In this scenario, the effects were drawn from a Multivariate Normal distribution with mean vector 0 and covariance matrix that achieves a per-trait variance of 1 and a correlation across traits of 1. This implies that the effects of the causal variants are equal across responses. Missing values were assigned to 80% of the individuals such that all missing value configurations across traits are equally likely for each individual. This resulted in the following proportion of missing cells in the phenotype matrix:
repz <- 1:20
scenarioz <- "08_full_equal_effects_indep_resid"
prefix <- "data/phenotypes/simulated/ukb_caucasian_white_british_unrel_100000_missing_pheno"
missingness <- vector("numeric", length(repz))
i <- 0
for(repp in repz){
i <- i+1
dat <- readRDS(paste0(prefix, "_", scenarioz, "_pheno_missing_", repp, ".rds"))
missingness[i] <- dat$prop_missing_cells
}
summary(missingness) Min. 1st Qu. Median Mean 3rd Qu. Max.
0.3981 0.3996 0.4004 0.4003 0.4008 0.4021 Here’s the methods comparison.
repz <- 1:20
prefix <- "output/prediction_accuracy/ukb_caucasian_white_british_unrel_100000_missing_pheno"
scenarioz <- "08_full_equal_effects_indep_resid"
methodz <- c("mr_mash_rss", "mvbayesC", "mvbayesC_rest", "wmt_sblup", "mtag_ldpred2_auto", "ldpred2_auto", "bayesR")
i <- 0
n_col <- 6
n_row <- length(repz) * length(scenarioz) * length(methodz) * length(traitz)
res <- as.data.frame(matrix(NA, ncol=n_col, nrow=n_row))
colnames(res) <- c("rep", "scenario", "method", "trait", "metric", "score")
for(sce in scenarioz){
for(met in methodz){
for(repp in repz){
dat <- readRDS(paste0(prefix, "_", sce, "_", met, "_pred_acc_", repp, ".rds"))
for(trait in traitz){
i <- i + 1
res[i, 1] <- repp
res[i, 2] <- sce
res[i, 3] <- met
res[i, 4] <- trait
res[i, 5] <- metric
res[i, 6] <- dat$r2[trait]
}
}
}
}
res <- transform(res, scenario=as.factor(scenario),
method=as.factor(method),
trait=as.factor(trait))
p_methods_shared <- ggplot(res, aes(x = trait, y = score, fill = method)) +
geom_boxplot(color = "black", outlier.size = 1, width = 0.85) +
stat_summary(fun=mean, geom="point", shape=23,
position = position_dodge2(width = 0.87,
preserve = "single")) +
ylim(0, 0.51) +
scale_fill_manual(values = c("pink", "red", "yellow", "orange", "green", "blue", "lightblue")) +
labs(x = "Trait", y = expression(italic(R)^2), fill="Method", title="") +
geom_hline(yintercept=0.5, linetype="dotted", linewidth=1, color = "black") +
theme_cowplot(font_size = 18)
print(p_methods_shared)Warning: Removed 1 row containing non-finite outside the scale range
(`stat_boxplot()`).Warning: Removed 1 row containing non-finite outside the scale range
(`stat_summary()`).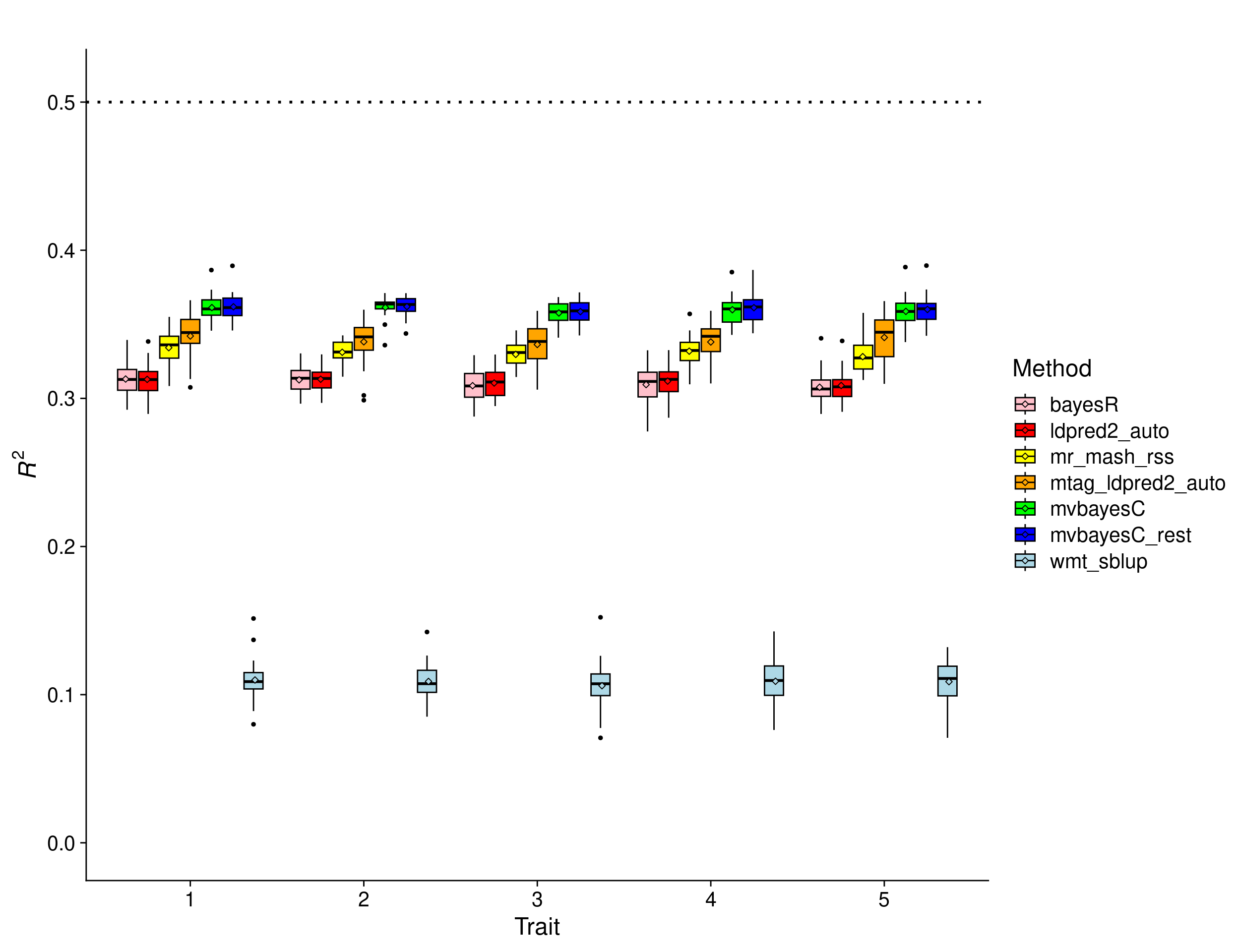
The results show that the performance of mr.mash-rss is now worse than the other multivariate methods, but still better than the univariate methods. This highlights that mr.mash-rss is not very robust to medium-high proportion of missing values.
sessionInfo()R version 4.1.2 (2021-11-01)
Platform: x86_64-pc-linux-gnu (64-bit)
Running under: Rocky Linux 8.5 (Green Obsidian)
Matrix products: default
BLAS/LAPACK: /opt/ohpc/pub/libs/gnu9/openblas/0.3.7/lib/libopenblasp-r0.3.7.so
locale:
[1] LC_CTYPE=en_US.UTF-8 LC_NUMERIC=C
[3] LC_TIME=en_US.UTF-8 LC_COLLATE=en_US.UTF-8
[5] LC_MONETARY=en_US.UTF-8 LC_MESSAGES=en_US.UTF-8
[7] LC_PAPER=en_US.UTF-8 LC_NAME=C
[9] LC_ADDRESS=C LC_TELEPHONE=C
[11] LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] cowplot_1.1.3 ggplot2_3.5.1
loaded via a namespace (and not attached):
[1] Rcpp_1.0.13 highr_0.11 pillar_1.9.0 compiler_4.1.2
[5] bslib_0.7.0 later_1.3.2 jquerylib_0.1.4 git2r_0.32.0
[9] workflowr_1.7.0 tools_4.1.2 digest_0.6.35 gtable_0.3.5
[13] jsonlite_1.8.8 evaluate_0.23 lifecycle_1.0.4 tibble_3.2.1
[17] pkgconfig_2.0.3 rlang_1.1.4 cli_3.6.2 rstudioapi_0.16.0
[21] yaml_2.3.8 xfun_0.44 fastmap_1.2.0 withr_3.0.0
[25] dplyr_1.1.4 stringr_1.5.1 knitr_1.47 generics_0.1.3
[29] fs_1.6.4 vctrs_0.6.5 sass_0.4.9 tidyselect_1.2.1
[33] rprojroot_2.0.4 grid_4.1.2 glue_1.7.0 R6_2.5.1
[37] fansi_1.0.6 rmarkdown_2.27 farver_2.1.2 magrittr_2.0.3
[41] whisker_0.4.1 scales_1.3.0 promises_1.3.0 htmltools_0.5.8.1
[45] colorspace_2.1-0 httpuv_1.6.11 labeling_0.4.3 utf8_1.2.4
[49] stringi_1.8.4 munsell_0.5.1 cachem_1.1.0